Mittelsenkrechte

Satz 1

Die drei Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.

\(m_a\), \(m_b\) und \(m_c\) sind die Mittelsenkrechten im Dreieck \(ABC\).

Motivation in der Schule

Die folgende interaktive Konstruktion enthält drei Strecken \(\overline{AB}\), \(\overline{BC}\) und \(\overline{CA}\) sowie deren Mittelsenkrechte. Die Schülerinnen und Schüler sollen diese drei Strecken zu einem Dreieck so zusammenfügen, dass die Punkte \(A\), \(B\) und \(C\) jeweils aufeinanderliegen.

Zwei der Mittelsenkrechten schneiden sich in einem Punkt (sofern die zugehörigen Strecken nicht parallel zueinander liegen). Bilden die drei Strecken ein Dreieck, so kann über die Eigenschaften der Mittelsenkrechten argumentriert werden, dass diese sich in einem Punkt schneiden. Die Schülerinnen und Schüler beobachten dies beim Zusammensetzen den Dreiecks.

Beweis von Satz 1

Enaktiver Zugang (spitzwinklige Dreiecke)

Der Schnittpunkt der Mittelsenkrechten kann auch gefaltet werden. Dazu wird ein spitzwinkliges Dreieck ausgeschnitten.

Anschließend werden zwei Ecken aufeinander gelegt und das Dreieck flach gedrückt. Ein Falz entsteht.

Beim Aufklappen erscheint der Falz als Mittelsenkrechte (Symmetrieachse) der entsprechenden Seite.

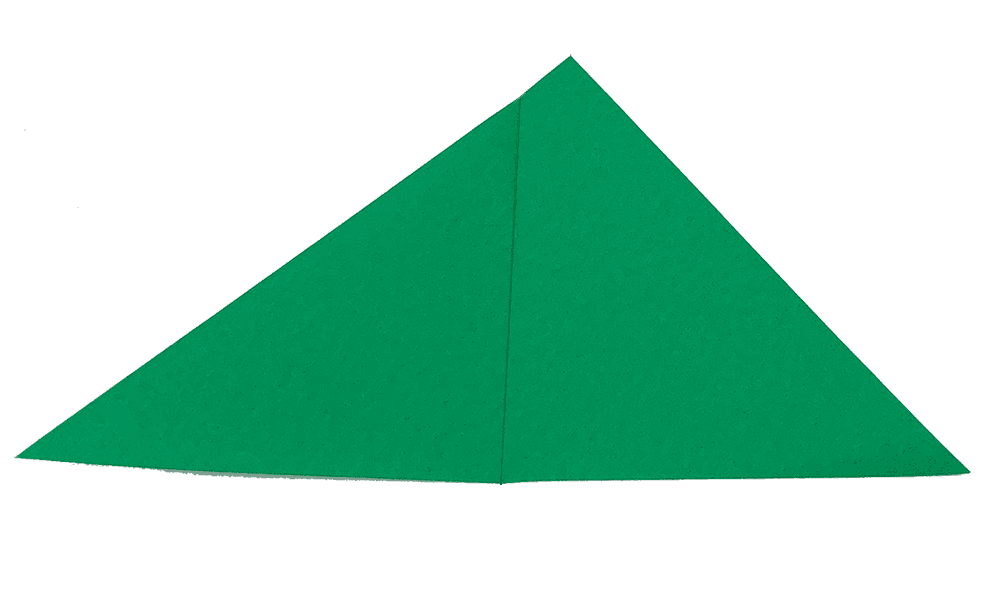
Schließlich wird bei den anderen Ecken ebenso verfahren. Die drei Falze (Mittelsenkrechte) verlaufen durch einem Punkt.

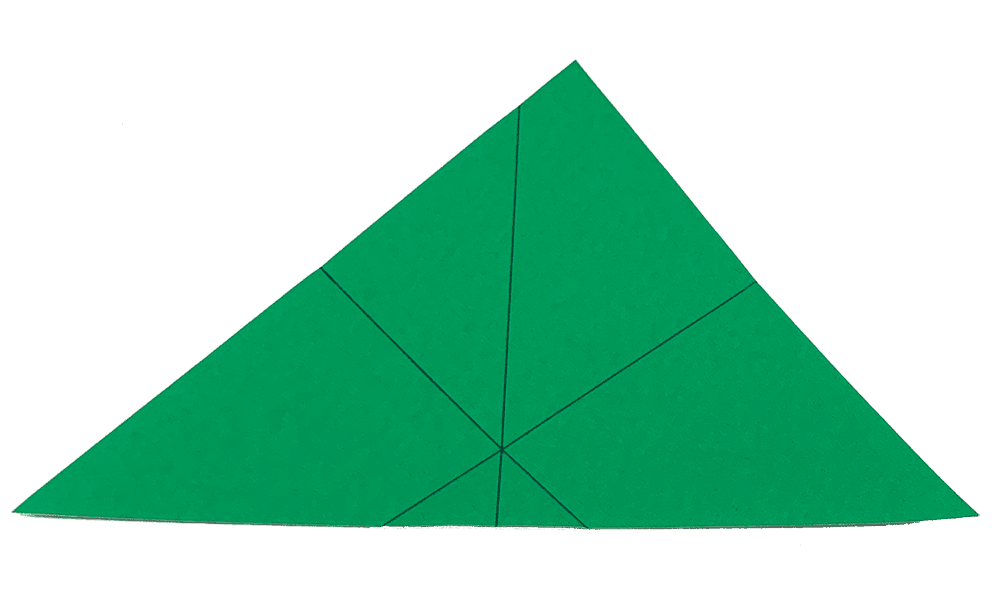
Folgerungen

a) Jedes Dreieck hat einen Umkreis. Sein Mittelpunkt ist der Schnittpunkt der Mittelsenkrechten.

b) Der Umkreismittelpunkt eines rechtwinkligen Dreiecks ist die Hypotenusenmitte.

Satz 2

Fällt man von einem beliebigen Punkt \(P\) des Umkreises die Lote auf die Dreiecksseiten, so sind die drei Lotfußpunkte kollinear.

Die Gerade wird auch Simson-Gerade (bzw. Wallace-Gerade) genannt. Der Satz ist umkehrbar:

Liegen die Lotfußpunkte von einem Punkt auf die (verlängerten) Seiten eines Dreiecks kollinear, so liegt der Punkt auf dem Umkreis des Dreiecks.

Beweis von Satz 2