Elementargeometrie
\(\)

Zielgruppe
Die Veranstaltung richtet sich vorwiegend an Studierende des Lehramts Realschule. Daher finden sich im Skript auch immer wieder Bemerkungen zum Geomtrieunterricht und möglicher Umsetzung der dargestellten Inhalte in der Schule. Diese Anmerkungen sind zwar nicht Bestandteil der Elementargeometrie, doch leisten Sie einen wertvollen Beitrag zur Verknüpfung vom Fachwissenschaft und Fachdidaktik.
Geometrie
Die historische Entwicklung der Geometrie prägt auch heute noch das Bild von Mathematik, auch in der Schule. "War die Geometrie in den ältesten Hochkulturen [...] eines unter anderen Anwendungsgebieten einer vorwiegend rechnerisch ausgerichteten Mathematik, so wurde sie in der griechischen Antike zum Kern und Hauptgebiet der gesamten Mathematik. Hier vollzog sich der in der Geschichte einmalige Wandel von einer auf Rezepten und vagen Begriffen beruhenden Praxis zu einer aus Definitionen, Axiomen und streng logisch bewiesenen Lehrsätzen bestehenden Theorie." [10, S. 1]. Dieses strukturierte Vorgehen spiegelt sich auch im Mathematikunterricht wider. Die Geometrie kombiniert Anschauung und Logik. Sie erlaubt die Beschreibung der Ebene und des dreidimensionalen Raumes.
Begriff
- Geometrie
| griechisch | deutsch |
|---|---|
| ge | Erde |
| metrein | messen |
| geometria | Erdmaße‚ Erdmessung‚ Landmessung |
-
Elementargeometrie
In der (Elementar-)Geometrie werden neue Aussagen aufgrund von Grundannahmen (Axiomen) und bereits gesicherter Aussagen getroffen. Hilfsmittel der Algebra bzw. Analysis stehen nicht zur Verfügung.elementar \( \neq \) einfach
Abgrenzung
Die Summe der Maße der Innenwinkel im Dreieck beträgt \( 180° \).
Diese Erkenntnis lässt sich einfach motivieren:
Beliebiges Dreieck zeichnen
Ein Dreieck wird auf Papier gezeichnet und die Innenwinkel werden beschriftet. Anschließend muss das Dreieck ausgeschnitten werden.

Ecken abreißen
Im nächsten Schritt werden die Ecken des Dreiecks abgerissen.
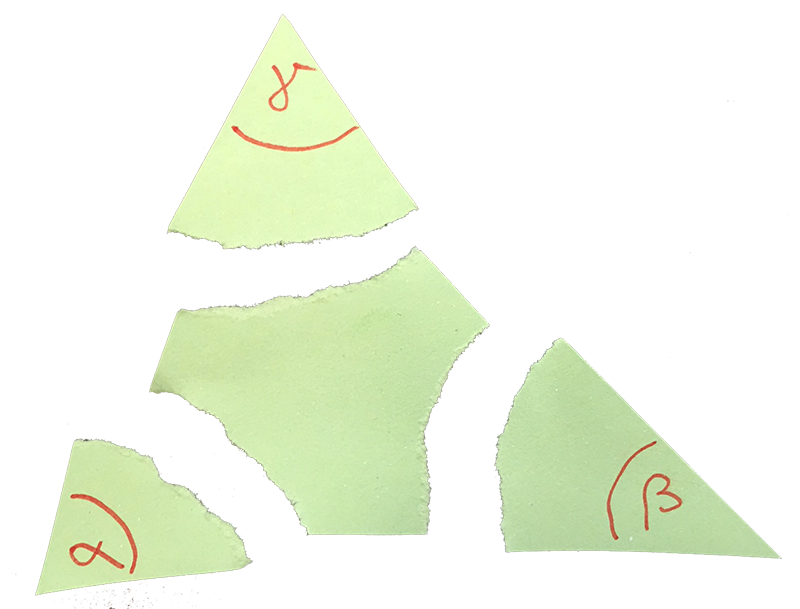
Ecken aneinanderlegen
Schießlich werden die Ecken des Dreiecks so bündig aneinandergelegt, dass die Eckpunkte aufeinanderliegen.

Es entsteht ein gestreckter Winkel. Die Vermutung lautet nun:
Beobachtung
Die Maße der drei Innenwinkel im gewählten Dreieck betragen zusammen \( 180° \).
Da etwa im Mathematikunterricht alle Schülerinnen und Schüler unterschiedliche Dreiecke gezeichnet haben, als Resultat jedoch immer ein gestreckter Winkel entsteht, liegt die Vermutung nahe, dass es sich um eine allgemeingültige Aussage handelt:
Vermutung
Die Summe der Maße der Innenwinkel beträgt in jedem Dreieck \( 180° \).
Diese Vermutung muss nun bewiesen werden, d. h. es muss eine lückenlose, widerspruchsfreie Argumentationskette angegeben werden. Die Vermutung wird dabei aus bereits bekannten Aussagen Schritt für Schritt hergeleitet.
Beweisidee
Durch einen Eckpunkt (hier \(C\)) wird eine Gerade \(g\) parallel zur gegenüberliegenden Dreiecksseite (hier \(\overline{AB}\)) betrachtet.
Beweisskizze
Es gelte \(g \parallel \overline{AB}\)
Wechselwinkelsatz an parallelen Geraden: \(\vert\alpha\vert= \vert\delta\vert\)
Wechselwinkelsatz an parallelen Geraden: \(\vert\beta\vert= \vert\epsilon\vert\)
Die Winkel \(\delta\), \(\gamma\) und \(\epsilon\) bilden an \(g\) einen gestreckten Winkel mit \(180°\).
\(\Rightarrow \vert\alpha\vert + \vert\beta\vert + \vert\gamma\vert = 180°\)
Fazit des Beispiels
Anhand des Beispiels der Summe der Maße der Innenwinkel des Dreiecks lässt sich sehr anschaulich eine Unterscheidung von didaktischem Handeln und elementargeometrischem Schließen aufzeigen.
Zunächst steht die Entdeckung des zuvor beschriebenen Zusammenhangs im Vordergrund. Dabei handelt es natürlich nicht um eine echte neue mathematische Entdeckung, sie wird im Unterricht jedoch als neu motiviert.
Die Summe der Innenwinkelmaße sticht als solches auch nicht direkt ist Auge, wie beispielsweise der rechte Winkel beim Satz des Thales. Daher ist eine didaktische Hinführung sinnvoll. Der handlungsorientierte Zugang bietet sich hier an.
Aus der "experimentellen" Beobachtung entwickelt sich im Unterrichtsgespräch eine Vermutung. Vielen Schülerinnen und Schülern genügt dieses Vorgehen als "Beweis" bzw. Nachweis: "Den Zusammenhang sieht man doch ... !"
Hier muss die Notwendigkeit eines allgemeingültigen Beweises als Teil des didaktischen Handelns herausgestellt werden. Dies führt im Unterricht oft zu Diskussionen, die jedoch zwingend geführt werden sollten, da hier ein wesentlicher Bestandteil mathematischen Handelns angesprochen wird.
Aus Sicht der Elementargeometrie liegt nun ein Satz (Aussage) vor, den es zu beweisen gilt. Dabei dürfen bekannte (bereits gezeigte) Aussagen verwendet werden, um durch logische Schlussfolgerungen zur gewünschten Aussage zu kommen.
Das Problem dabei ist jedoch, dass nicht alle genutzen Aussagen beweisbar sind. Es gibt Grundannahmen, bei denen dies nicht gelingt. Dabei handelt es sich um die so genannten Axiome. Diese müssen vorausgesetzt werden, damit elementargeometrisches Arbeiten überhaupt möglich ist. Im gezeigten Beispiel ist die Tatsache, dass genau eine durch Punkt \(C\) verlaufende parallele Gerade zur Geraden (Strecke) \(AB\) existiert, solch ein Axiom (Parallelenaxiom). Dies kann nicht bewiesen werden und muss daher als Grundannahme gelten.
Externes Video
Michael Gieding: Was ist in Axiom? (12.05.2018)
Dieses eingebundene Video stammt von einem externen Anbieter. Es kann Werbung sowie Verweise auf andere Videos und Inhalte enthalten. Bezug genommen wird hier nur das ursprünglich eingebundene Video. (Stand: 18.10.2021)
Struktur
Der Aufbau und die Struktur in diesem Skripts orientieren sich an folgender Quelle:
H. Schupp, Figuren und Abbildungen, Hildesheim: div-Verlag franzbecker, 1998
(v1.35 – 09.01.2023)